TOPIC 1: NUMBERS
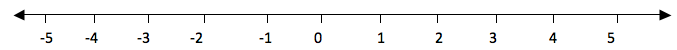
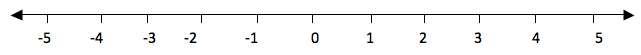
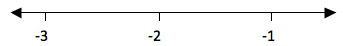
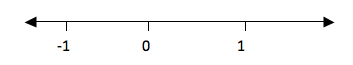
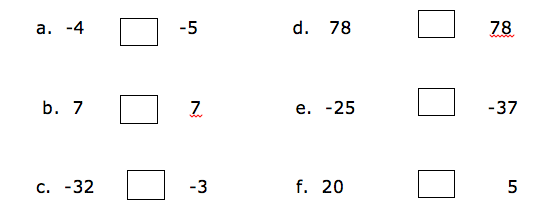
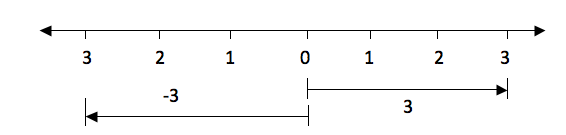
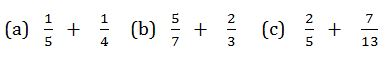
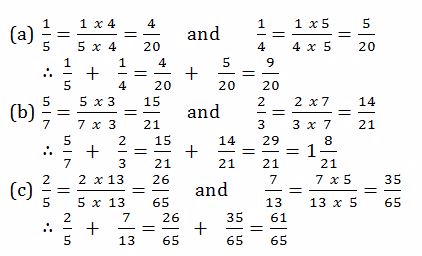
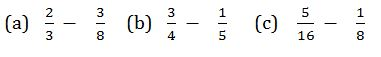
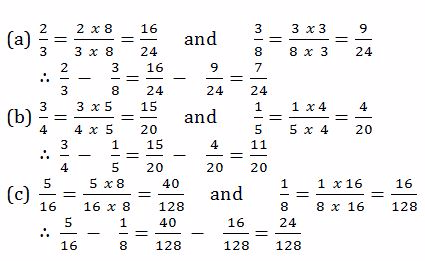
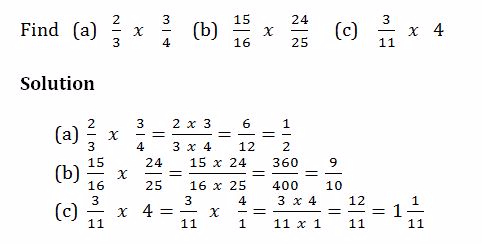
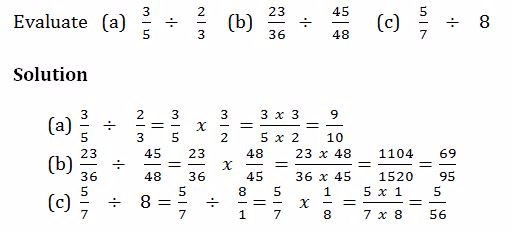
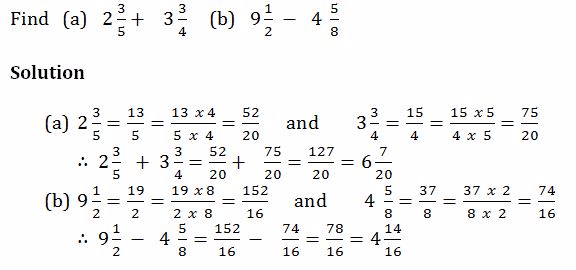
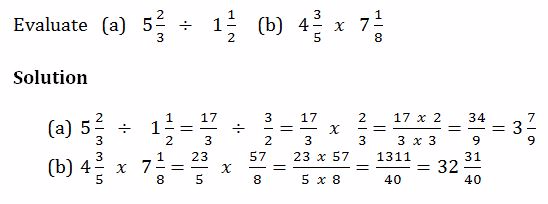

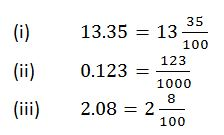
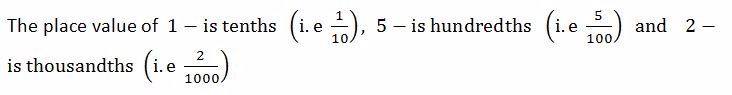
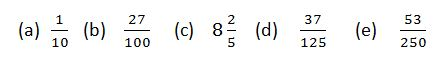
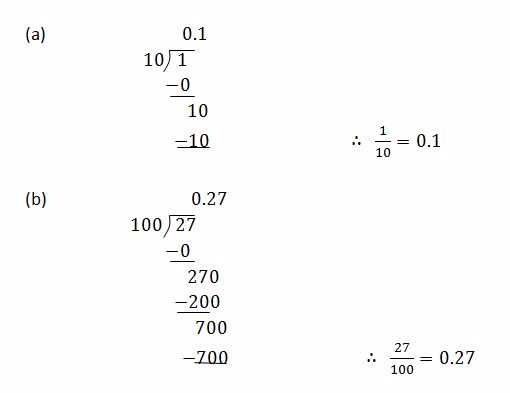



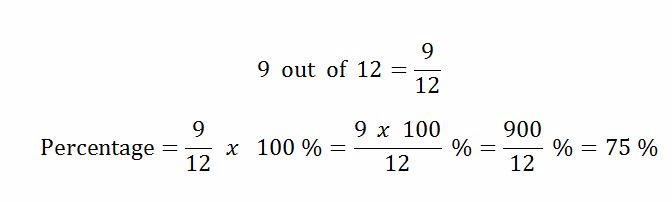
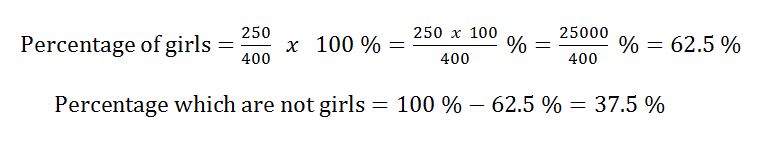 TOPIC 7: ALGEBRA
TOPIC 7: ALGEBRA

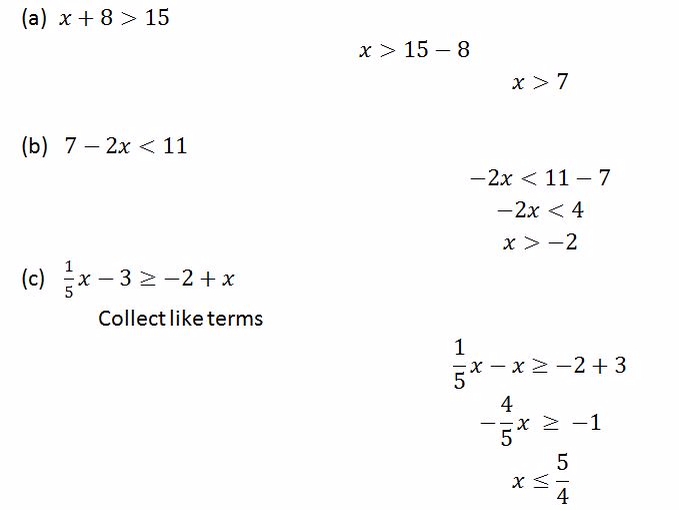
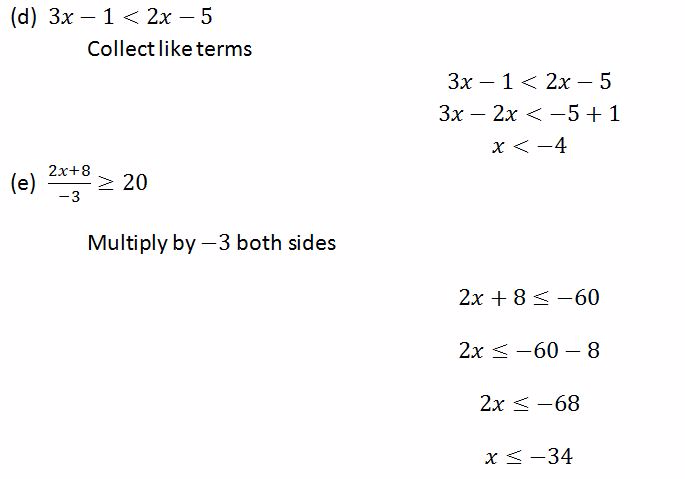
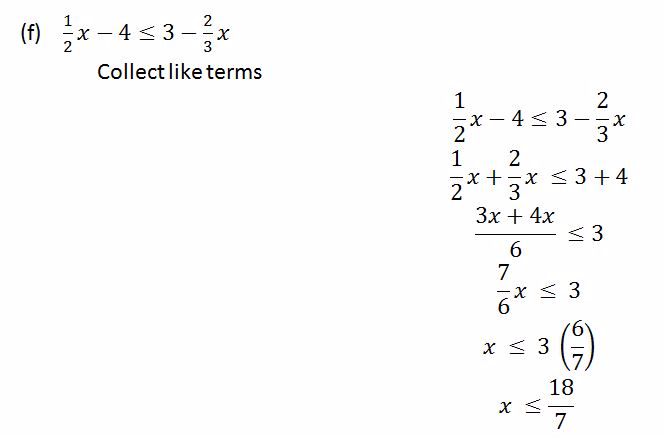

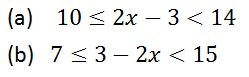

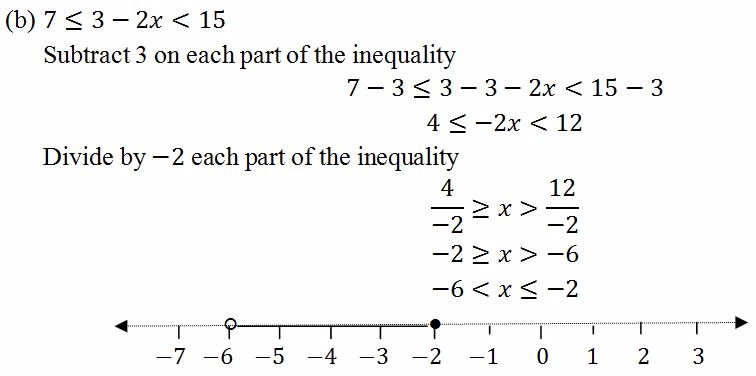
TOPIC 8: NUMBERS
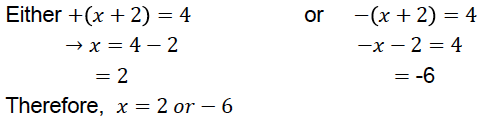
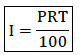
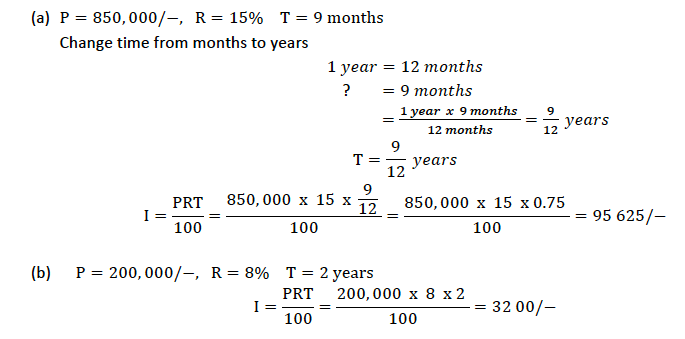
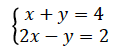
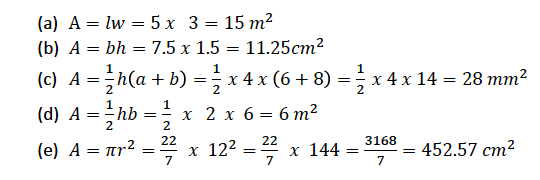
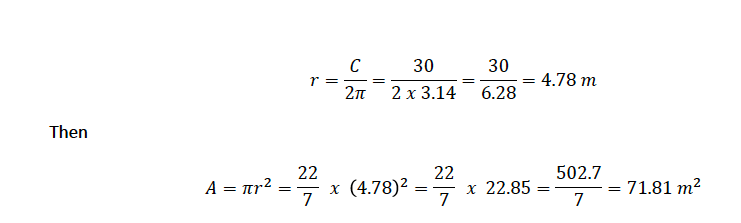
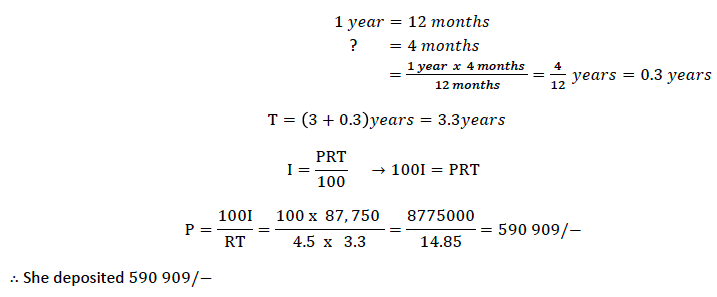
we
know that when we count we start 1,2 .... . But there are other numbers
like 0, negative numbers and decimals. All these types of numbers are
categorized in different groups like counting numbers, integers,real
numbers, whole numbers and rational and irrational numbers according to
their properties. all this have been covered in this chapter
Integers
Identify integers
Consider a number line below
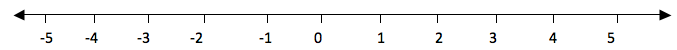
The
numbers from 0 to the right are called positive numbers and the numbers
from 0 to the left with minus (-) sign are called negative numbers.
Therefore all numbers with positive (+) or negative (-) sign are called
integers and they are denoted by Ζ. Numbers with positive sign are
written without showing the positive sign. For example +1, +2, +3, …
they are written simply as 1, 2, 3, … . But negative numbers must carry
negative sign (-). Therefore integers are all positive and negative
numbers including zero (0). Zero is neither positive nor negative
number. It is neutral.
The
numbers from zero to the right increases their values as the increase.
While the numbers from zero to the left decrease their values as they
increase. Consider a number line below.
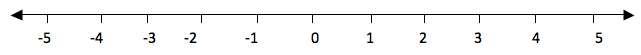
If
you take the numbers 2 and 3, 3 is to the right of 2, so 3 is greater
than 2. We use the symbol ‘>’ to show that the number is greater than
i. e. 3 >2(three is greater than two). And since 2 is to the left of
3, we say that 2 is smaller than 3 i.e. 2<3. The symbol ‘<’ is
use to show that the number is less than.
Consider
numbers to the left of 0. For example if you take -5 and -3. -5 is to
the left of -3, therefore -5 is smaller than -3. -3 is to the right of
-5, therefore -3 is greater than -5.
Generally, the number which is to the right of the other number is greater than the number which is to the left of it.
If
two numbers are not equal to each to each other, we use the symbol ‘≠’
to show that the two numbers are not equal. The not equal to ‘≠’ is the
opposite of is equal to ‘=’.
Example 21
Represent the following integers Ζ on a number line
- 0 is greater than Ζ and Ζ is greater than -4
- -2 is less than Ζ and Ζ is less than or equal to 1.
Solution
a.
0 is greater than Ζ means the integers to the left of zero and Ζ is
greater than -4 means integers to the left of -4. These numbers are -1,
-2 and -3. Consider number line below
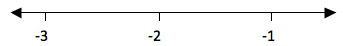
b.
-2 is less than Ζ means integers to the right of -2 and Ζ is less than
or equal to 1 means integers to the left of 1 including 1. These
integers are -1, 0 and 1. Consider the number line below
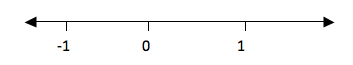
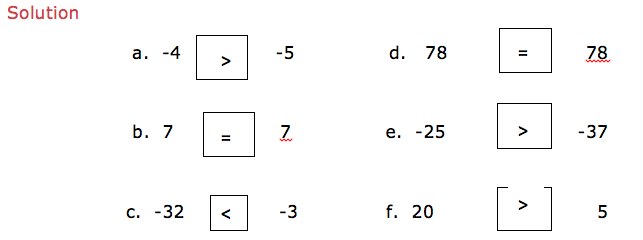
Example 22
Put the signs ‘is greater than’ (>), ‘is less than’ (<), ‘is equal to’ (=) to make a true statement.
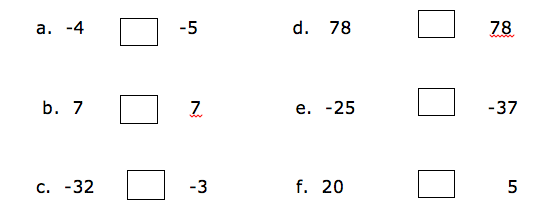

Addition of Integers
Add integers
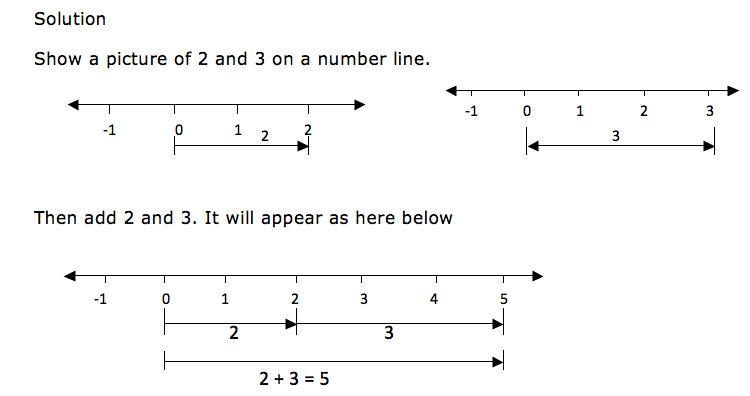
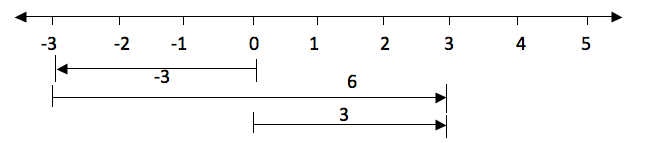
Example 23
2 + 3
Show a picture of 2 and 3 on a number line.

When
drawing integers on a number line, the arrows for the positive numbers
goes to the right while the arrows for the negative numbers goes to the
left. Consider an illustration bellow.
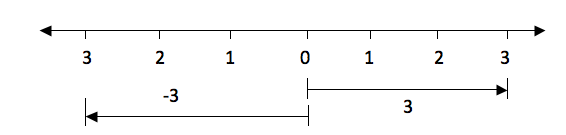
The
distance from 0 to 3 is the same as the distance from 0 to -3, only the
directions of their arrows differ. The arrow for positive 3 goes to the
right while the arrow for the negative 3 goes to the left.
Example 24
-3 + 6
Solution

Subtraction of Integers
Subtract integers
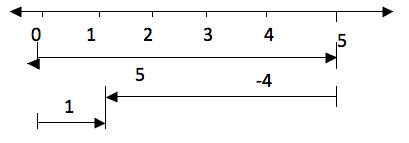
Since
subtraction is the opposite of addition, if for example you are given
5-4 is the same as 5 + (-4). So if we have to subtract 4 from 5 we can
use a number line in the same way as we did in addition. Therefore 5-4
on a number line will be:

Take five steps from 0 to the right and then four steps to the left from 5. The result is 1.
Multiplication of Integers
Multiply integers
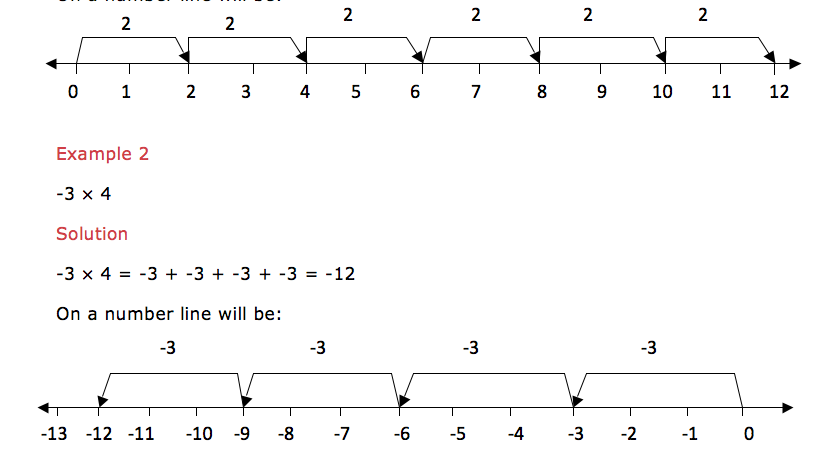
Example 25
2×6 is the same as add 2 six times i.e. 2×6 = 2 + 2 + 2 + 2 + 2 +2 = 12. On a number line will be:

Multiplication
of a negative integer by a negative integer cannot be shown on a number
line but the product of these two negative integers is a positive
integer.
From
the above examples we note that multiplication of two positive integers
is a positive integer. And multiplication of a positive integer by a
negative integer is a negative integer. In summary:
- (+)×,(+) = (+)
- (-)×,(-) = (+)
- (+)×,(-) = (-)
- (-)×,(+) = (-)
Division of Integers
Divide integers
Example 26
6÷3 is the same as saying that, which number when you multiply it by 3 you will get 6, that number is 2, so, 6÷3 = 2.
Therefore
division is the opposite of multiplication. From our example 2×3 = 6
and 6÷3 = 2. Thus multiplication and division are opposite to each
other.
Dividing
two integers which are both positive the quotient (answer) is a
positive integer. If they are both negative also the quotient is
positive. If one of the integer is positive and the other is negative
then the quotient is negative. In summary:
- (+)÷(+) = (+)
- (-)÷(-) = (+)
- (+)÷(-) = (-)
- (-)÷(+) = (-)
Mixed Operations on Integers
Perform mixed operations on integers
You
may be given more than one operation on the same problem. Do
multiplication and division first and then the rest of the signs. If
there are brackets, we first open the brackets and then we do division
followed by multiplication, addition and lastly subtraction. In short we
call it BODMAS. The same as the one we did on operations on whole
numbers.
Example 27
9÷3 + 3×2 -1 =
Solution
9÷3 + 3×2 -1
=3 + 6 -1 (first divide and multiply)
=8 (add and then subtract)
Example 28
(12÷4 -2) + 4 – 7=
Solution
(12÷4 -2) + 4 – 7
=1 + 4 – 7 (do operations inside the brackets and divide first)
=5 – 7 (add)
=2
TOPIC 2: FRACTIONS
A fraction is a number which is expressed in the form of a/b where a - is the top number called numerator and b- is the bottom number called denominator.
Addition of Fractions
Add fractions
Operations on fractions involves addition, subtraction, multiplication and division
- Addition and subtraction of fractions is done by putting both fractions under the same denominator and then add or subtract
- Multiplication of fractions is done by multiplying the numerator of the first fraction with the numerator of the second fraction, and the denominator of the first fraction with the denominator the second fraction.
- For mixed fractions, convert them first into improper fractions and then multiply
- Division of fractions is done by taking the first fraction and then multiply with the reciprocal of the second fraction
- For mixed fractions, convert them first into improper fractions and then divide
Example 11
Find
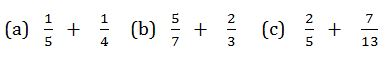
Solution
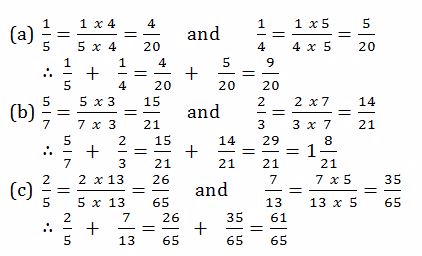
Subtraction of Fractions
Subtract fractions
Example 12
Evaluate
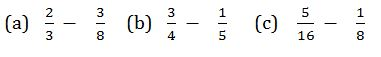
Solution
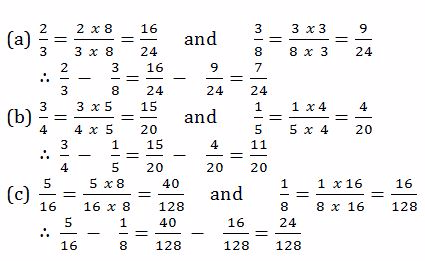
Multiplication of Fractions
Multiply fractions
Example 13
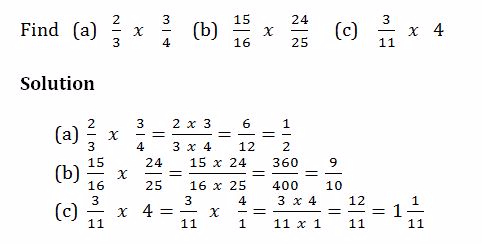
Division of Fractions
Divide fractions
Example 14
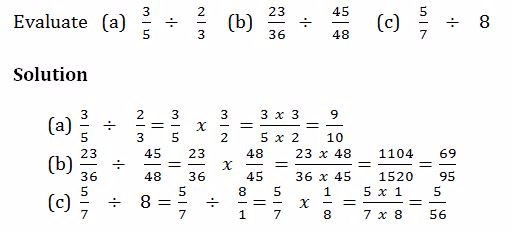
Mixed Operations on Fractions
Perform mixed operations on fractions
Example 15
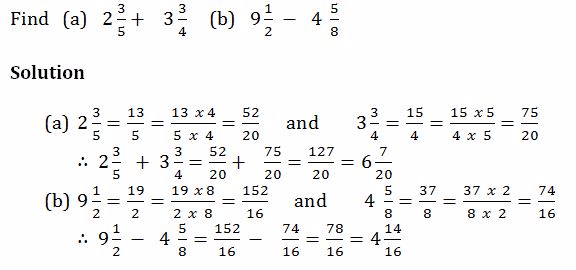
Example 16
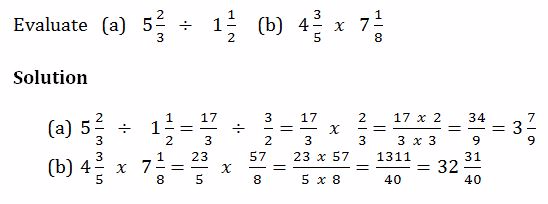
Word Problems Involving Fractions
Solve word problems involving fractions
Example 17
- Musa is years old. His father is 3¾times as old as he is. How old is his father?
- 1¾of a material are needed to make suit. How many suits can be made from
TOPIC 3: DECIMAL AND PERCENTAGE
The Concept of Decimals
Explain the concept of decimals
A
decimal- is defined as a number which consist of two parts separated by
a point.The parts are whole number part and fractional part
Example 1

Example 2
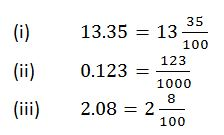
Conversion of Fractions to Terminating Decimals and Vice Versa
Convert fractions to terminating decimals and vice versa
The first place after the decimal point is called tenths.The second place after the decimal point is called hundredths e.t.c
Consider the decimal number 8.152
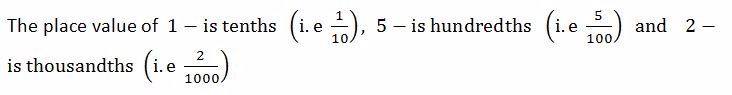
NOTE
- To convert a fraction into decimal, divide the numerator by denominator
- To convert a decimal into fraction, write the digits after the decimal point as tenths, or hundredths or thousandths depending on the number of decimal places.
Example 3
Convert the following fractions into decimals
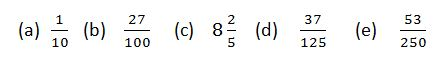
Solution
Divide the numerator by denominator
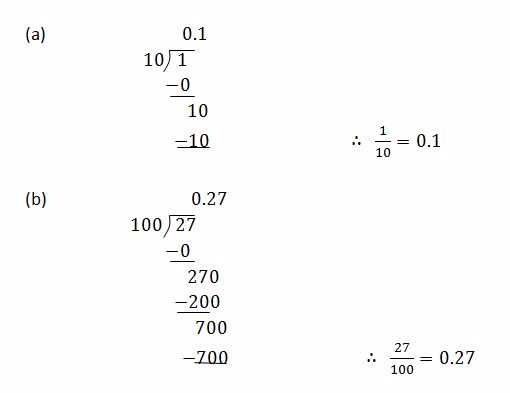
Expressing a Quantity as a Percentage
Express a quantity as a percentage
The
percentage of a quantity is found by converting the percentage to a
fraction or decimal and then multiply it by the quantity.
Example 9

NOTE:The
concept of percentage of a quantity can be used to solve the problems
involving percentage increase and decrease as shown in the below
examples:-
A Fractions into Percentage and Vice Versa
Convert a fraction into percentage and vice versa
To change a fraction or a decimal into a percentage, multiply it by 100%
Example 10
Convert the following fractions into percentages

A Decimal into Percentage and Vice Versa
Convert a decimal into percentage and vice versa
To change a percentage into a fraction or a decimal, divide it by 100%
Example 11
Convert the following percentages into decimals

Percentages in Daily Life
Apply percentages in daily life
Example 12
In an assignment, Regina scored 9 marks out of 12. Express this as a percentage
Solution
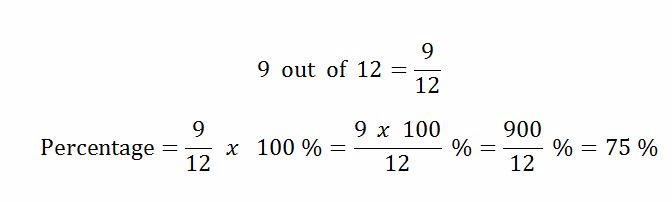
Example 13
A school has 400 students of which 250 are girls. What percentage of the students are not girls?
Solution
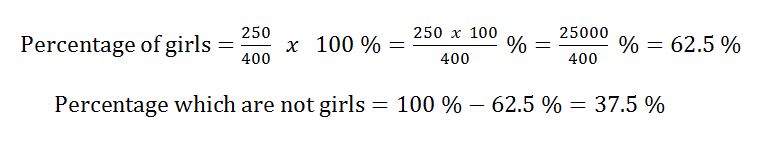 TOPIC 7: ALGEBRA
TOPIC 7: ALGEBRA
An
algebraic expression – is a collection of numbers, variables, operators
and grouping symbols.Variables - are letters used to represent one or
more numbers
An
inequality – is a mathematical statement containing two expressions
which are not equal. One expression may be less or greater than the
other.The expressions are connected by the inequality symbols<,>,≤
or≥.Where< = less than,> = greater than,≤ = less or equal and ≥ =
greater or equal.
Linear Inequalities with One Unknown
Solve linear inequalities in one unknown
An
inequality can be solved by collecting like terms on one side.Addition
and subtraction of the terms in the inequality does not change the
direction of the inequality.Multiplication and division of the sides of
the inequality by a positive number does not change the direction of the
inequality.But multiplication and division of the sides of the
inequality by a negative number changes the direction of the inequality
Example 11
Solve the following inequalities

Solution
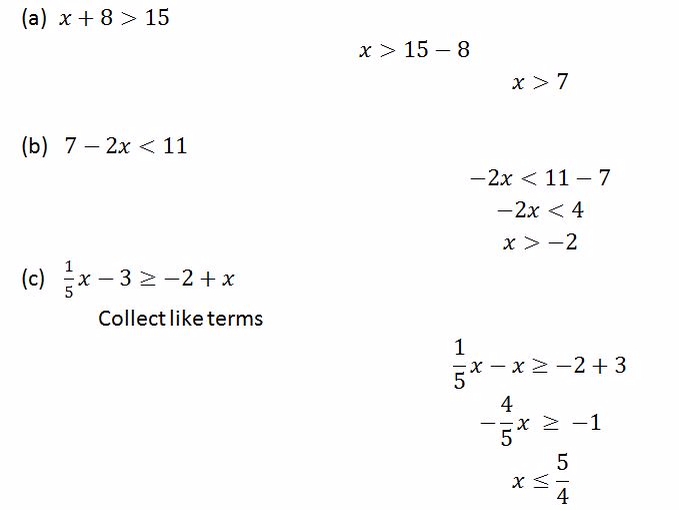
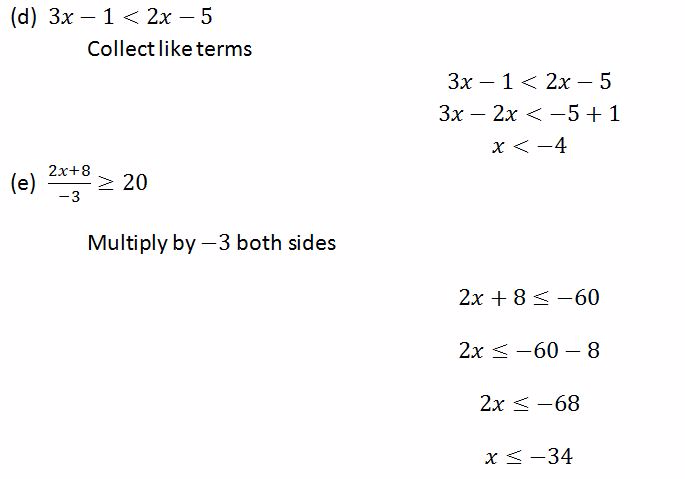
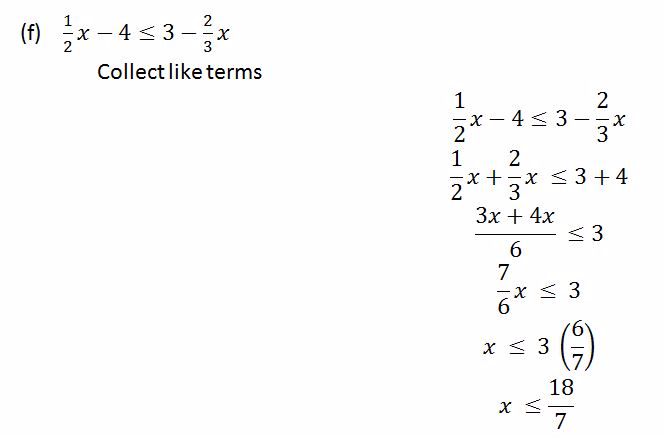
Linear Inequalities from Practical Situations
Form linear inequalities from practical situations
To represent an inequality on a number line, the following are important to be considered:
- The endpoint which is not included is marked with an empty circle
- The endpoint which is included is marked with a solid circle
Example 12

Compound statement – is a statement made up of two or more inequalities
Example 13
Solve the following compound inequalities and represent the answer on the number line
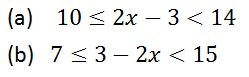
Solution

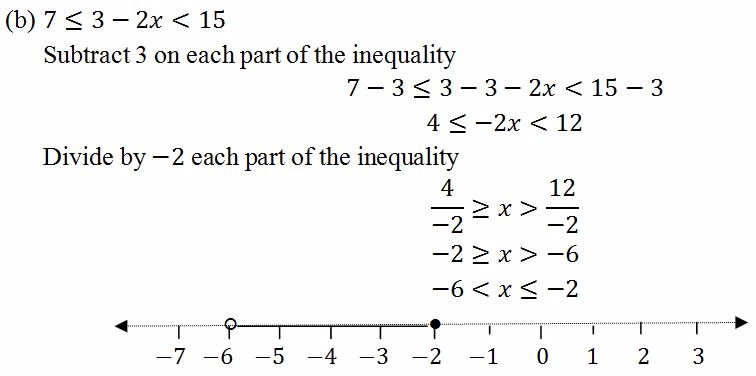
TOPIC 8: NUMBERS
A Rational Number
Define a rational number
ARational Numberis a real number that can be written as a simple fraction (i.e. as aratio). Most numbers we use in everyday life are Rational Numbers.
| Number | As a Fraction | Rational? |
|---|---|---|
| 5 | 5/1 | Yes |
| 1.75 | 7/4 | Yes |
| .001 | 1/1000 | Yes |
| -0.1 | -1/10 | Yes |
| 0.111... | 1/9 | Yes |
| √2(square root of 2) | ? | NO ! |
The square root of 2 cannot be written as a simple fraction! And there are many more such numbers, and because they arenot rationalthey are calledIrrational.
The Basic Operations on Rational Numbers
Perform the basic operations on rational numbers
Addition of Rational Numbers:
To
add two or morerational numbers, the denominator of all the rational
numbers should be the same. If the denominators of all rational numbers
are same, then you can simply add all the numerators and the denominator
value will the same. If all the denominator values are not the same,
then you have to make the denominator value as same, by multiplying the
numerator and denominator value by a common factor.
Example 1
1⁄3+4⁄3=5⁄3
1⁄3 +1⁄5=5⁄15 +3⁄15 =8⁄15
Subtraction of Rational Numbers:
To
subtract two or more rational numbers, the denominator of all the
rational numbers should be the same. If the denominators of all rational
numbers are same, then you can simply subtract the numerators and the
denominator value will the same. If all the denominator values are not
the same, then you have to make the denominator value as same by
multiplying the numerator and denominator value by a common factor.
Example 2
4⁄3 -2⁄3 =2⁄3
1⁄3-1⁄5=5⁄15-3⁄15=2⁄15
Multiplication of Rational Numbers:
Multiplication
of rational numbers is very easy. You should simply multiply all the
numerators and it will be the resulting numerator and multiply all the
denominators and it will be the resulting denominator.
Example 3
4⁄3x2⁄3=8⁄9
Division of Rational Numbers:
Division
of rational numbers requires multiplication of rational numbers. If you
are dividing two rational numbers, then take the reciprocal of the
second rational number and multiply it with the first rational number.
Example 4
4⁄3÷2⁄5=4⁄3x5⁄2=20⁄6=10⁄3
Real Numbers
Real Numbers
Define real numbers
he
type of number we normally use, such as 1, 15.82, −0.1, 3/4,
etc.Positive or negative, large or small, whole numbers or decimal
numbers are all Real Numbers.
They are called "Real Numbers" because they are not Imaginary Numbers.
Absolute Value of Real Numbers
Find absolute value of real numbers
The
absolute value of a number is the magnitude of the number without
regard to its sign. For example, the absolute value of 𝑥 𝑜𝑟 𝑥
written as 𝑥 . The sign before 𝑥 is ignored. This is because the
distance represented is the same whether positive or negative. For
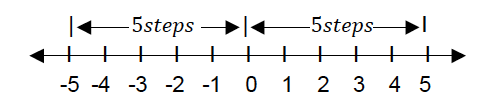
example, a student walking 5 steps forward or 5 steps backwards will be
considered to have moved the same distance from where she originally
was, regardless of the direction.

The 5 steps forward (+5) and 5 steps backward (-5) have an absolute value of 5
Thus |𝑥| = 𝑥 when 𝑥 is positive (𝑥 ≥ 0), but |𝑥| = −𝑥 when 𝑥 is negative (𝑥 ≤ 0).
For example, |3| = 3 since 3 is positive (3 ≥ 0) And −3 = (−3) =3 since −3 is negative (3 ≤ 0)
Related Practical Problems
Solve related practical problems
Example 5
Solve for 𝑥 𝑖𝑓 |𝑥| = 5
Solution
For any number 𝑥, |𝑥| = 5, there are two possible values. Either 𝑥,= +5 𝑜𝑟 𝑥 = 5
Example 6
Solve for 𝑥, given that |𝑥 + 2| =4
Solution
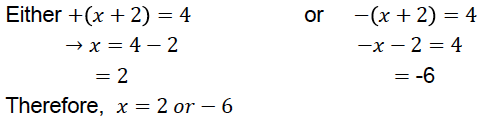
TOPIC 9: RATIO, PROFIT AND LOSS.
Ratio
Simple Interest
Calculate simple interest
The amount of money charged when a person borrows money e. g from a bank is called interest (I)
The amount of money borrowed is called principle (P)
To calculate interest, we use interest rate (R) given as a percentage and is usually taken per year or per annum (p.a)
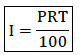
Example 6
Calculate the simple interest charged on the following
- 850, 000/− at 15% per annum for 9 months
- 200, 000/− at 8% per annum for 2 years
Solution
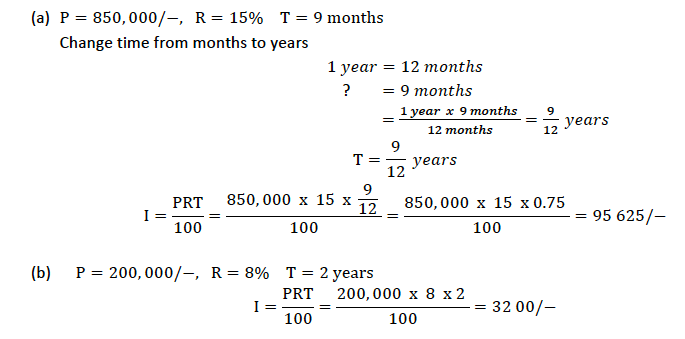
Real Life Problems Related to Simple Interest
Solve real life problems related to simple interest
Example 7
Mrs.
Mihambo deposited money in CRDB bank for 3 years and 4 months. A t the
end of this time she earned a simple interest of 87, 750/− at 4.5% per
annum. How much had she deposited in the bank?
Solution
Given I = 87, 750/− R = 4.5% % T = 3 years and 4 months
Change months to years
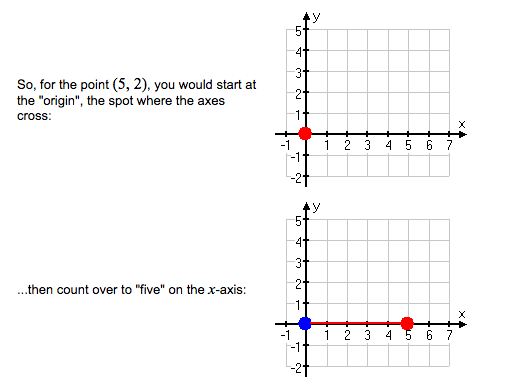
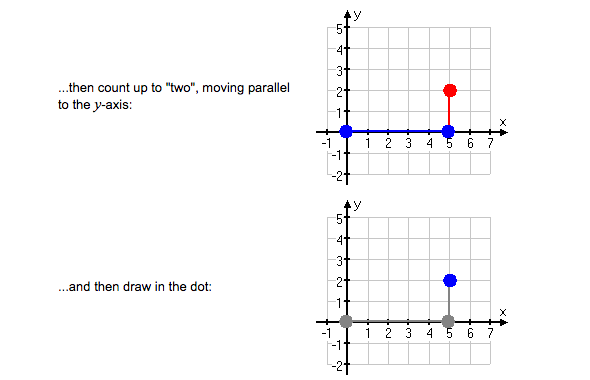
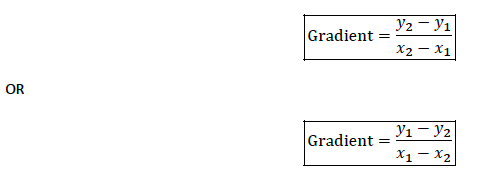
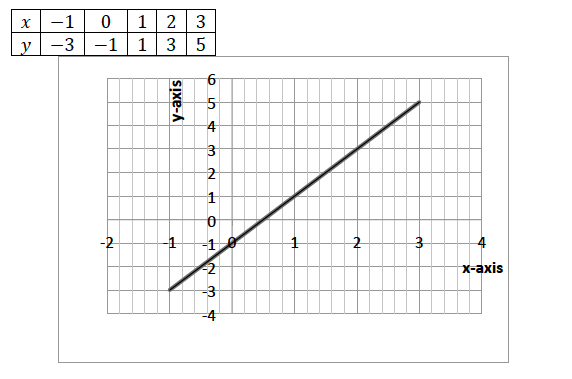
TOPIC 10: COORDINATE OF A POINT
Read the coordinates of a point
Simultaneous Equations
Linear Simultaneous Equations Graphically
Solve linear simultaneous equations graphically
Use
the intercepts to plot the straight lines of the simultaneous
equations. The point where the two lines cross each other is the
solution to the simultaneous equations
Example 7
Solve the following simultaneous equations by graphical method
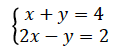
Solution
Consider: 𝑥 + 𝑦 = 4
If 𝑥 = 0, 0 + 𝑦 = 4 𝑦 = 4
If 𝑦 = 0, 𝑥 + 0 = 4 𝑥 = 4
Draw a straight line through the points 0, 4 and 4, 0 on the 𝑥𝑦 − plane
Consider: 2𝑥 − 𝑦 = 2
If 𝑥 = 0, 0 − 𝑦 = 2 𝑦 = −2
If 𝑦 = 0, 2𝑥 − 0 = 2 𝑥 = 1
Draw a straight line through the points (0,−2) and (1, 0) on the 𝑥𝑦 − plane

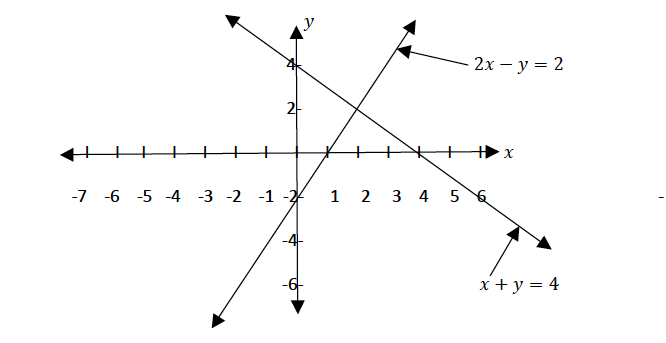
From the graph above the two lines meet at the point 2, 2 , therefore 𝑥 = 2 𝑎𝑛𝑑 𝑦 = 2
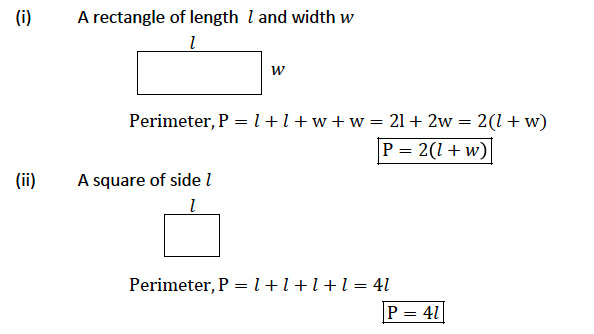
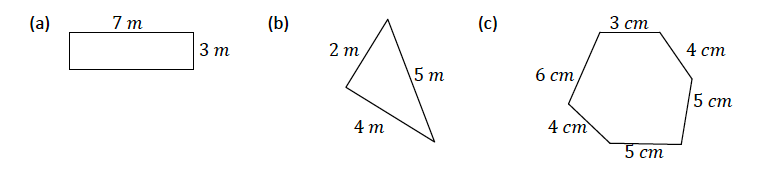
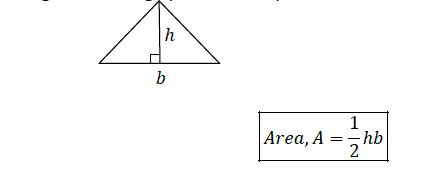
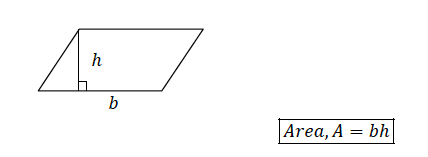
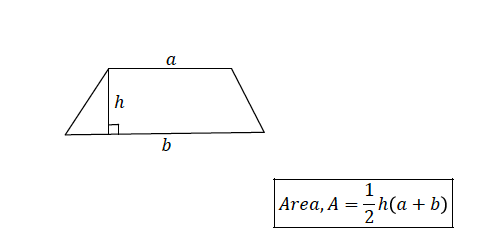
TOPIC 11: PERIMETERS AND AREAS
Perimeters of Triangles and Quadrilaterals
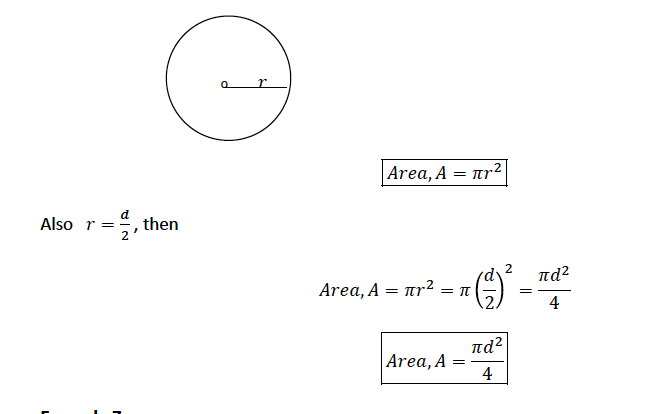
Areas of Circle
Calculate areas of circle
Consider a circle of radius r;

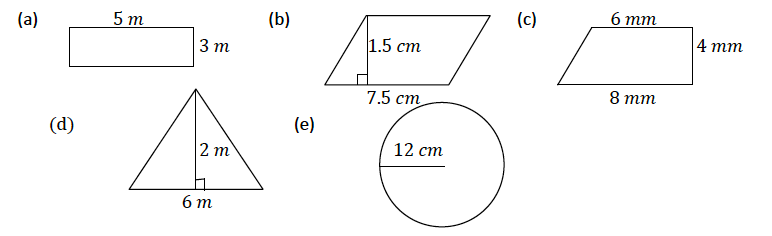
Example 5
Find the areas of the following figures

Solution
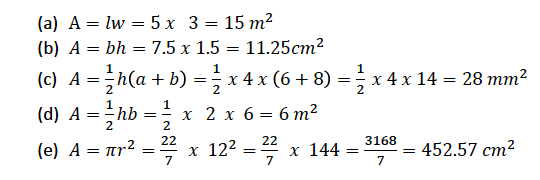
Example 6
A circle has a circumference of 30 𝑚. What is its area?
Solution
Given circumference, 𝐶 = 30 𝑚
C = 2𝜋𝑟
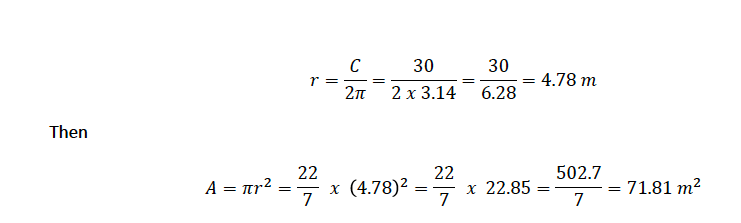
Ndugu mwalimu/mwanafunzi kama unapata changamoto yoyote ile
kuhusu upatikanaji wa NOTES HIZI kwenye website hii, tafadhari wasiliana nasi kwa
simu no/hotline. 0759-104804 Paschal kabonge
barua pepe. paschalkabonge2@gmail.com
au andika maoni yako kwenye sehemu ya comment hapa chini ya post hii.
Kumbuka: mitihani yote inapatikana bureeee kabisa.
Asante.
ELIMU NI HAKI KWA WOTE.
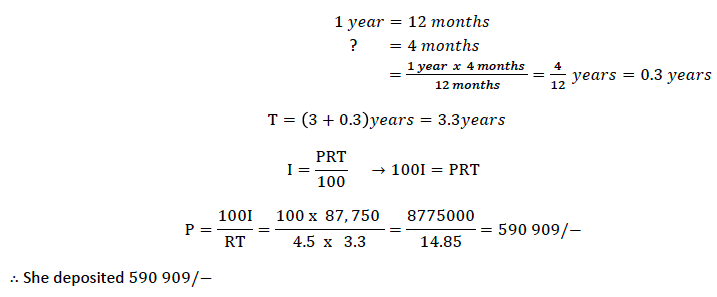




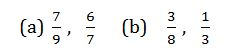
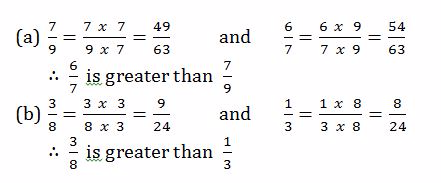
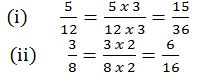

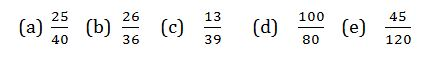

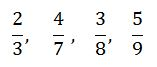
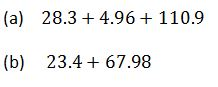
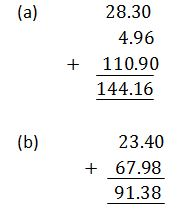
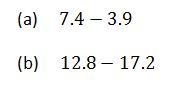
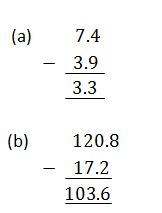
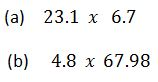
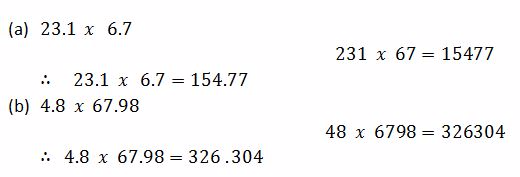
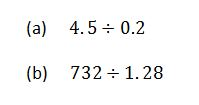
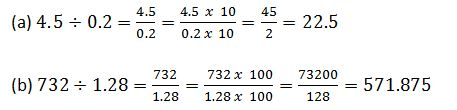
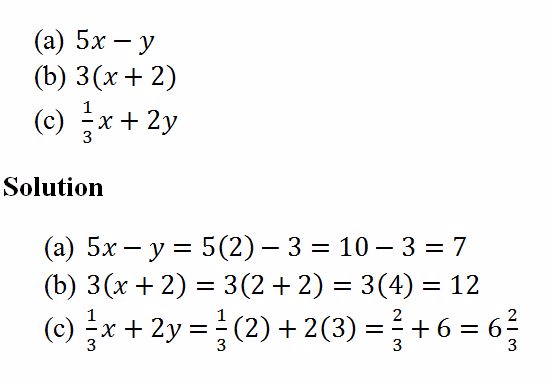
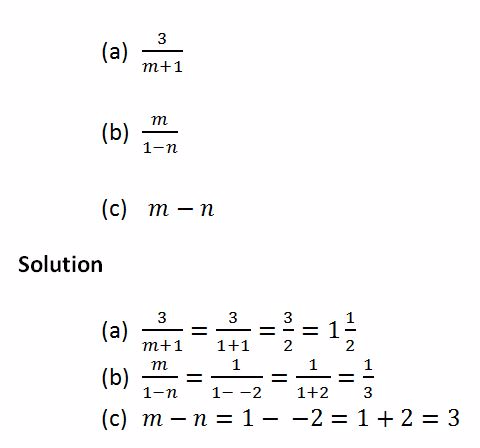
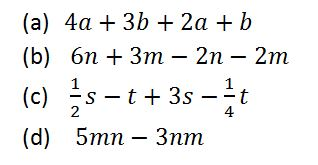
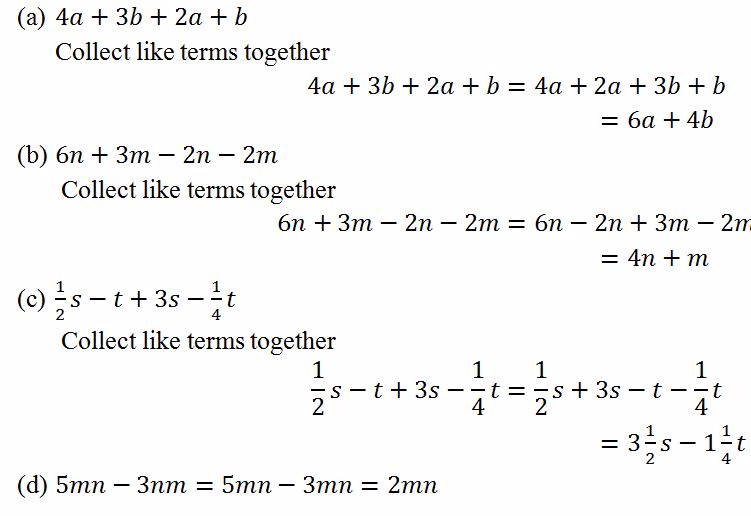
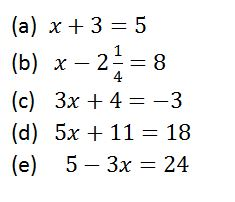
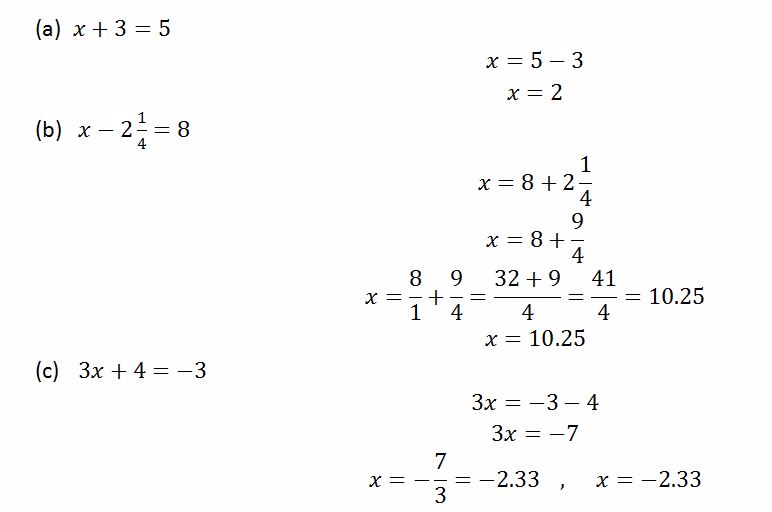
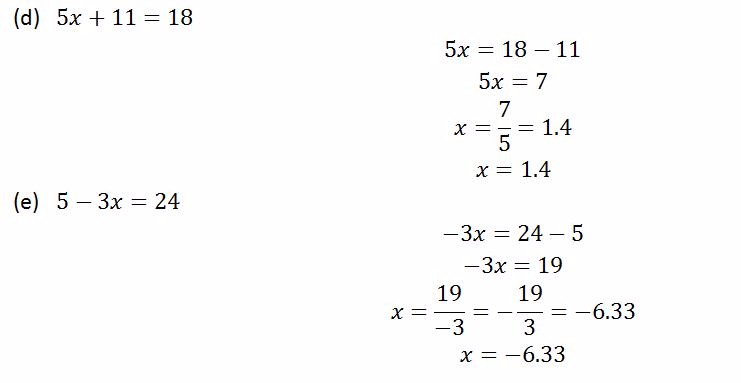
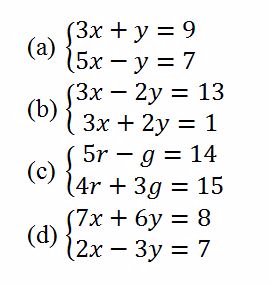
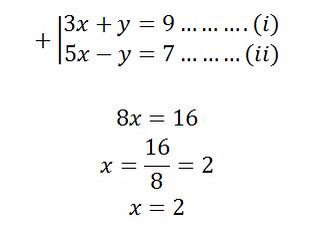

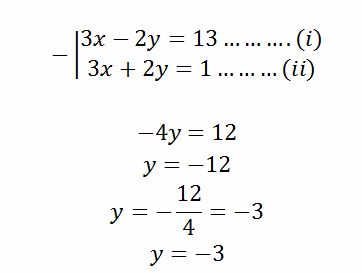
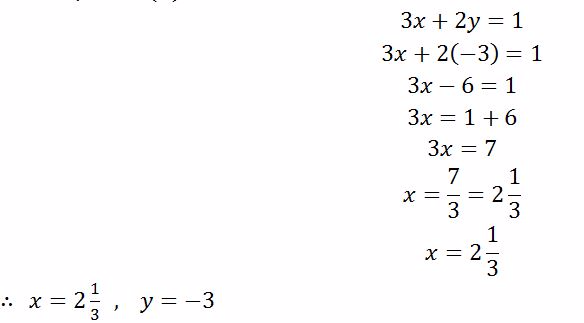
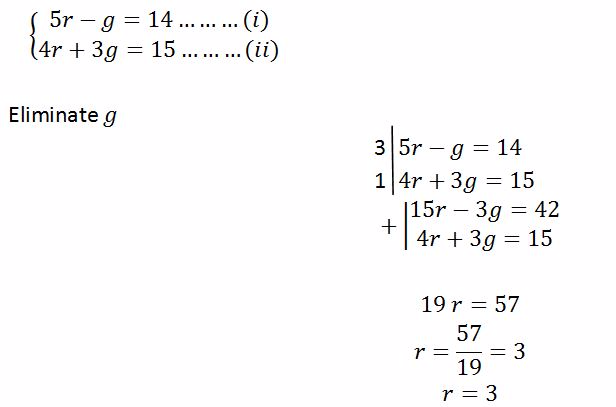
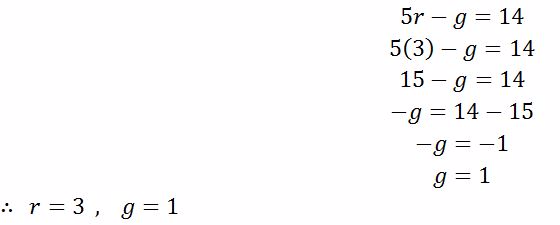
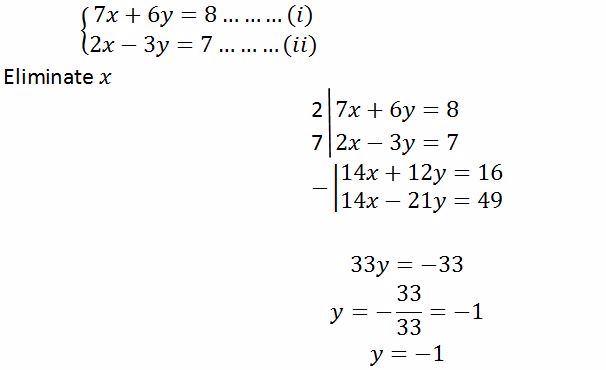
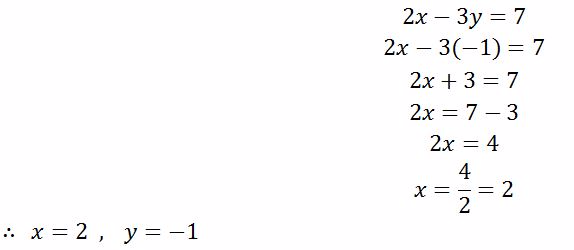
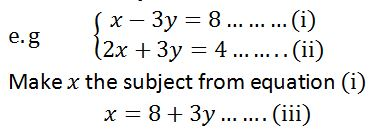
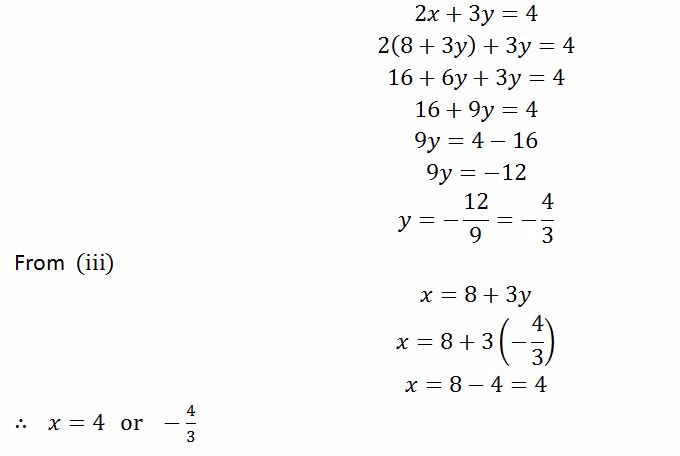
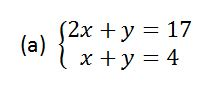
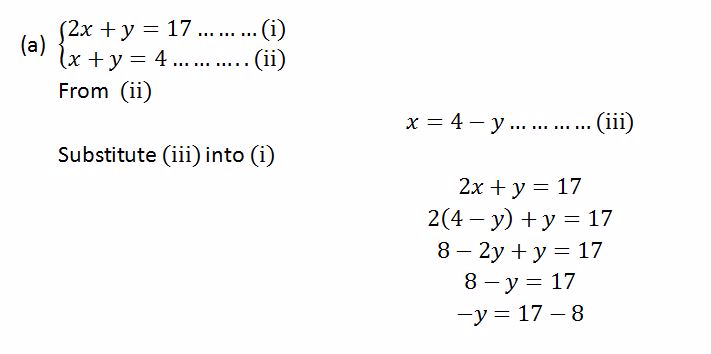
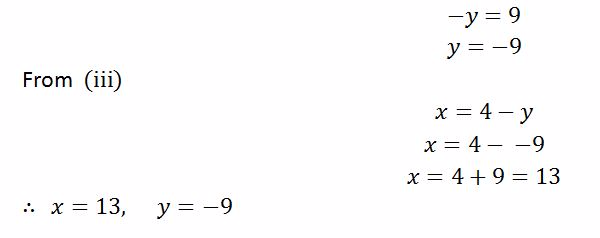
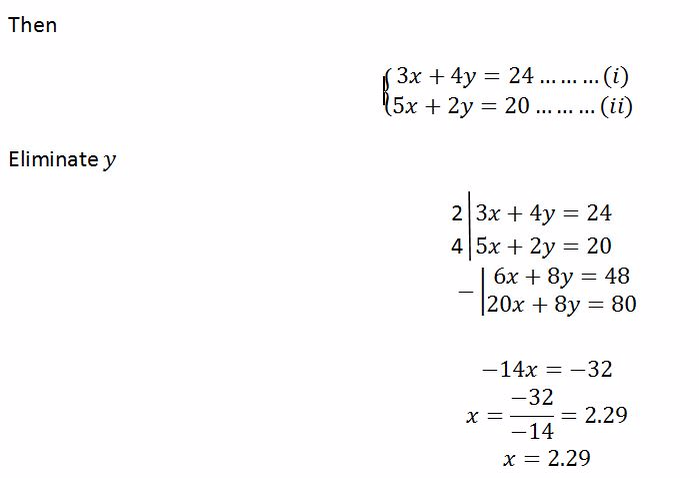
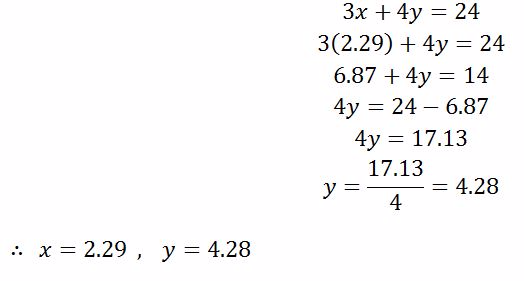





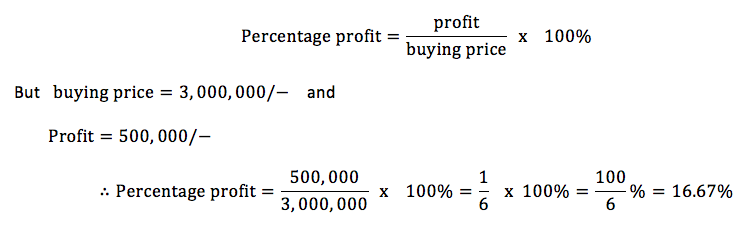

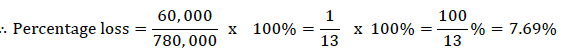


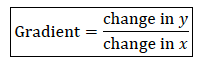
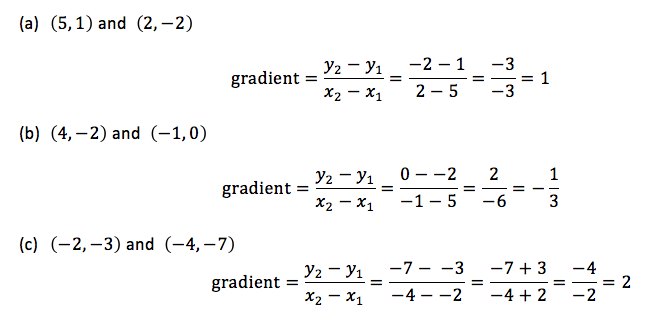
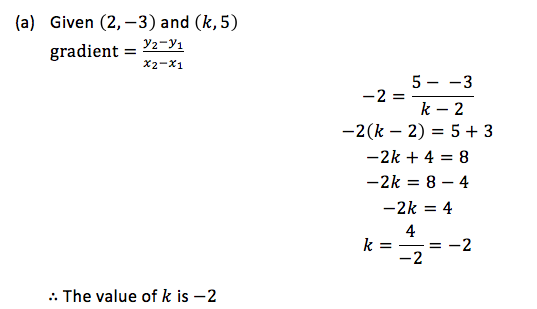
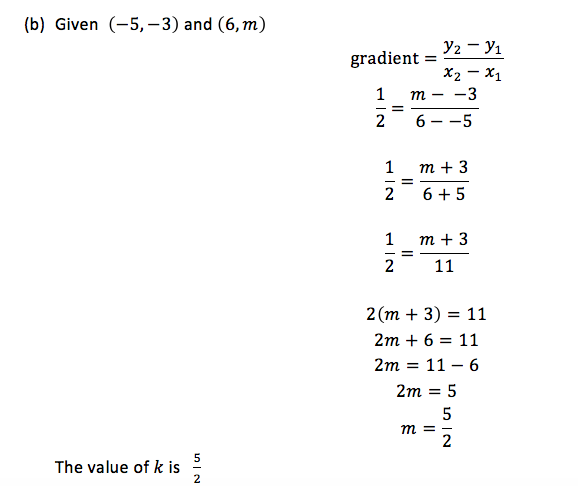
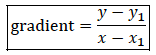
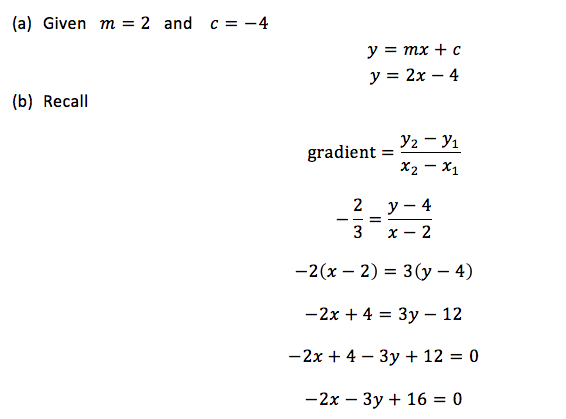


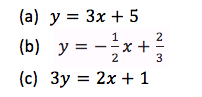



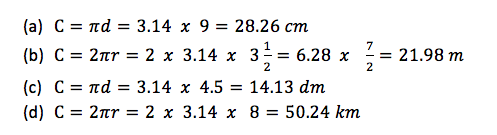
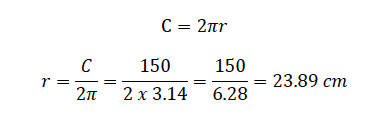


8 Comments
This is very helpful
ReplyDeleteThank you for visiting our website.
DeleteMathematics Form One Full Notes >>>>> Download Now
Delete>>>>> Download Full
Mathematics Form One Full Notes >>>>> Download LINK
>>>>> Download Now
Mathematics Form One Full Notes >>>>> Download Full
>>>>> Download LINK z3
Nice notes
ReplyDeleteHuda Mustaphe
ReplyDeleteGood
ReplyDeleteThank you for visiting our website.
DeleteMathematics Form One Full Notes >>>>> Download Now
ReplyDelete>>>>> Download Full
Mathematics Form One Full Notes >>>>> Download LINK
>>>>> Download Now
Mathematics Form One Full Notes >>>>> Download Full
>>>>> Download LINK px